内容参考 《算法竞赛入门经典-训练指南》
二叉索引树(Binary Indexed Tree, BIT),俗称树状数组,又以发明者命名为Fenwick树。现多用于高效计算数列的前缀和,区间和。 树状数组-维基百科。
应用
给定一个n个元素的数组 ,设计一个查询操作Query(i, j) = 。 如何做?如果用前缀和的思想,计算,那么 Query(i, j) = ,单次查询时间为O(1),但是如果需要更新的话,那每次更新,都需要更新一批,会很慢,所以需要二叉索引树,它解决这个问题的更新及查询的时间复杂度都是O(logn)。
Lowbit函数
定义Lowbit(x) 为 x 的二进制表达式中最右边的1所对应的值。如88的二进制是101 1000, 所以lowbit(88) = 8(二进制是1000),实现中用lowbit(x) = x & -x。因为计算机中整数采用补码存储,因此 -x 是 x 按位取反,末尾加1以后的结果。两者按位与之后,前面的变为0,就可以得到lowbit。
构造BIT树
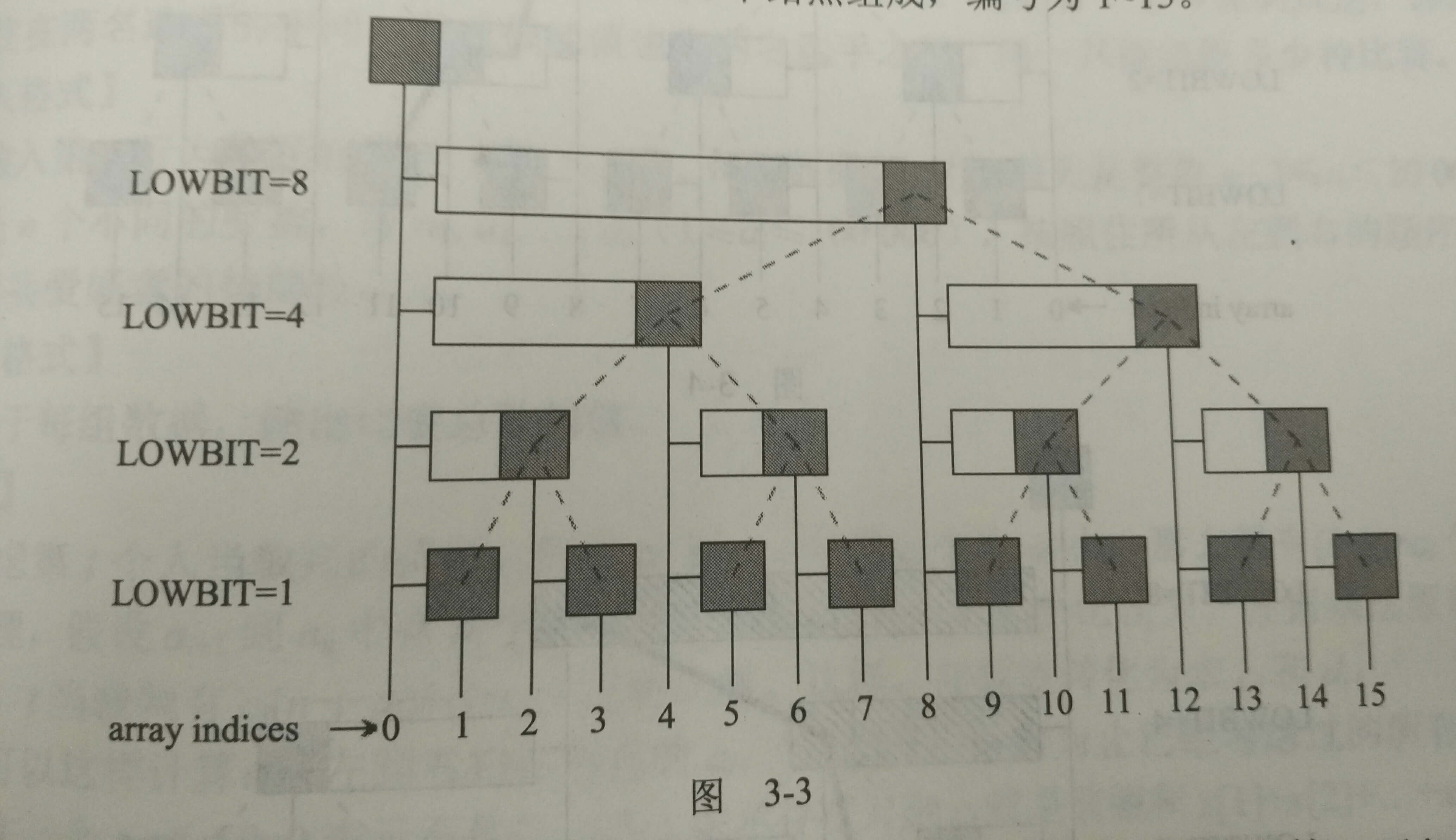
如图3-3所示,对于节点i,如果它是左子结点,那么父节点的编号就是i + lowbit(i);如果它是右子节点,那么父节点的编号是i - lowbit(i)。需要注意编号为0的点是虚拟节点。之后的定义的数组的序号也是从1 ~ n。
构造一个辅助数组 ,即是A数组中的一段连续和,例如。
求前缀和,在树中从节点i往左上走,把经过的累加。
修改,在树中从节点i往右上走,边走边修改。如下图所示。
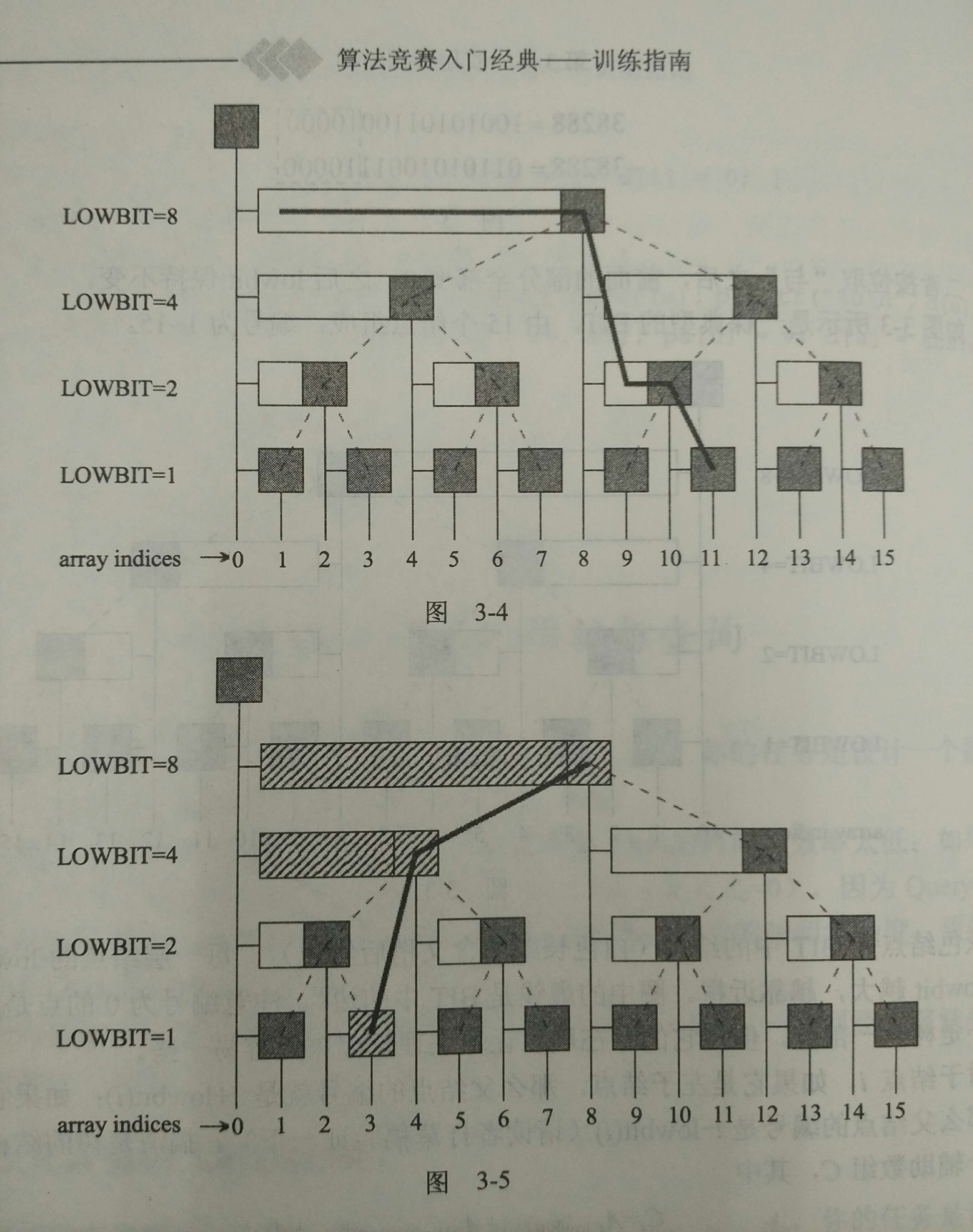
两个操作的代码:
// 求和
int sum(int x) {
int ret = 0;
while (x > 0) {
ret += C[x];
x -= lowbit(x);
}
return ret;
}
// 修改,让A[x] 增加d
void add(int x, int d) {
while (x <= n ) {
C[x] += d;
x += lowbit(x);
}
}
练习
307. Range Sum Query - Mutable - leetcode
线段树(区间树)
线段树与二叉索引树结构类似,单次查询和更新的时间复杂度也是。不过线段树能求解的问题范围更大一些,比如区间和,区间最值,能用二叉索引树解的一般也能用线段树解。待完善。。。
上面那个leetcode 307用线段树始终超时。。。
另外327. Count of Range Sum 的线段树解是在没看懂。。
参考: